Computerized Boolean Expression
Submitted By: Dipak Koley (Department of BCA, Batch: 2016-2019)
A Boolean expression tree is used to represent Boolean expression. Boolean expression tree consists of Binary operator(s) such as AND (.), OR (+), XOR (⊕), XNOR (⊙) or Unary operator NOT ( ' ) or both of them. As Boolean expression tree belongs to binary tree, each node contains less than or equal to two sub Childs. Every parent node contains a Boolean operator and each leaf node contains variable or constant value like true (1) or false (0).Every Parent node can have maximum two sub Childs, and the parent node containing unary operators can have maximum one sub-child. Leaf node cannot have sub child.
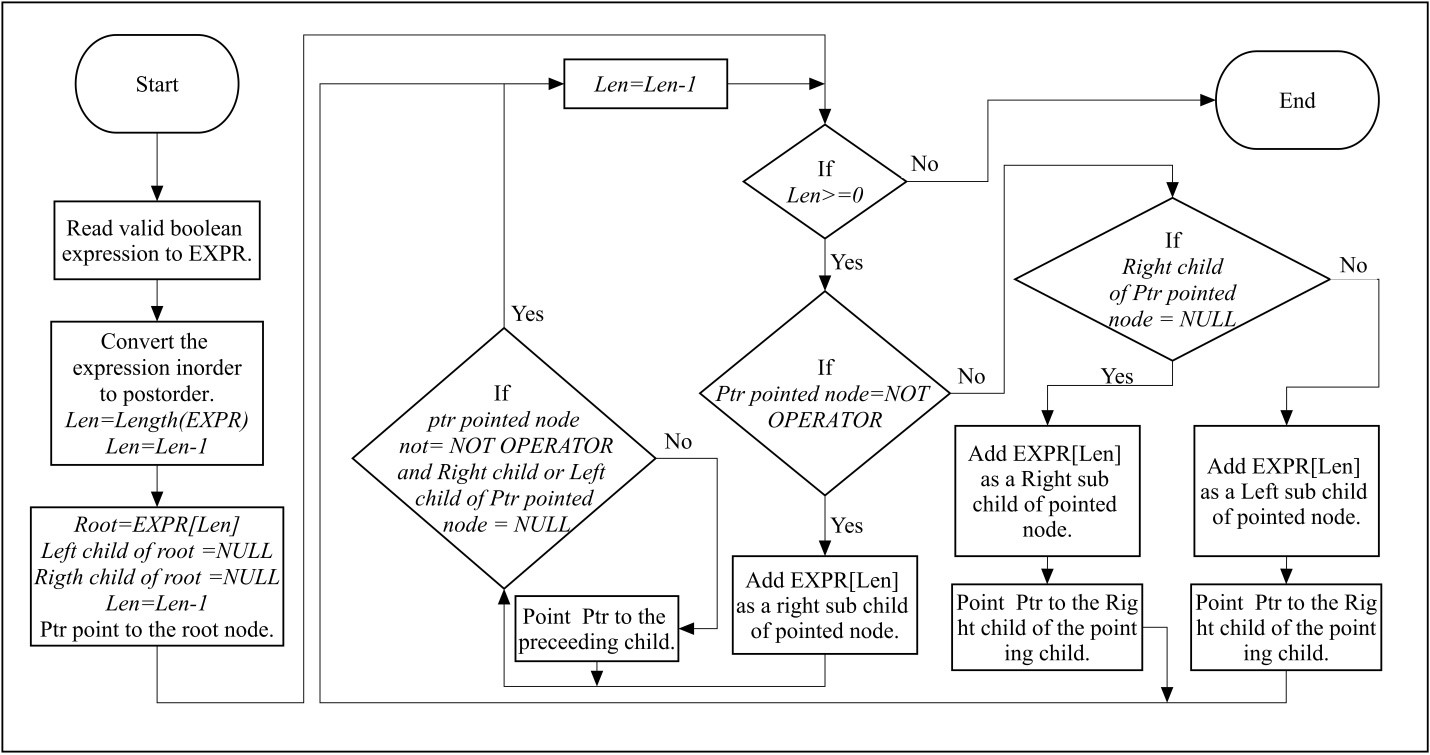
The main purpose of construction of a binary tree is to evaluate Boolean expression through computer. To create a Boolean expression tree we need to input a valid Boolean expression. Then convert the Boolean expression from in-order to post-order. Then read the post order expression from right to left and construct the expression tree. Expression tree can also be created by converting the expression from in-order to pre-order. In case of pre order we need to read the converted expression from left to right and then create the expression tree.
Algorithm
1.0 Input Boolean Expression to exp
2.0 Convert the exp from inorder to postorder
3.0 Len=length (exp)-1
4.0 Create Root node of tree containing exp[Len] and set it as current node
5.0 Len=Len-1
6.0 While Len>=0 do
6.1 Create a node which contains exp[Len]
6.2.0 If current node cannot contains right child then
6.2.1 Make the new node as the Right child of current node
6.3.0 Else
6.3.1.0 If current node ≠ Unary operator then
6.3.1.1 Make the new node as the Left child of current node
6.3.2.0 Else
6.3.2.1 Search for parent node which does not contain more than one child and parent node ≠ Unary operator
6.3.2.2 Set the searched node as current node
6.3.2.3 Make the new node as the Left child of current node
6.3.3 End if
6.4 End if
6.5 Len=Len-1
6.6 End Loop
Flowchart
Example

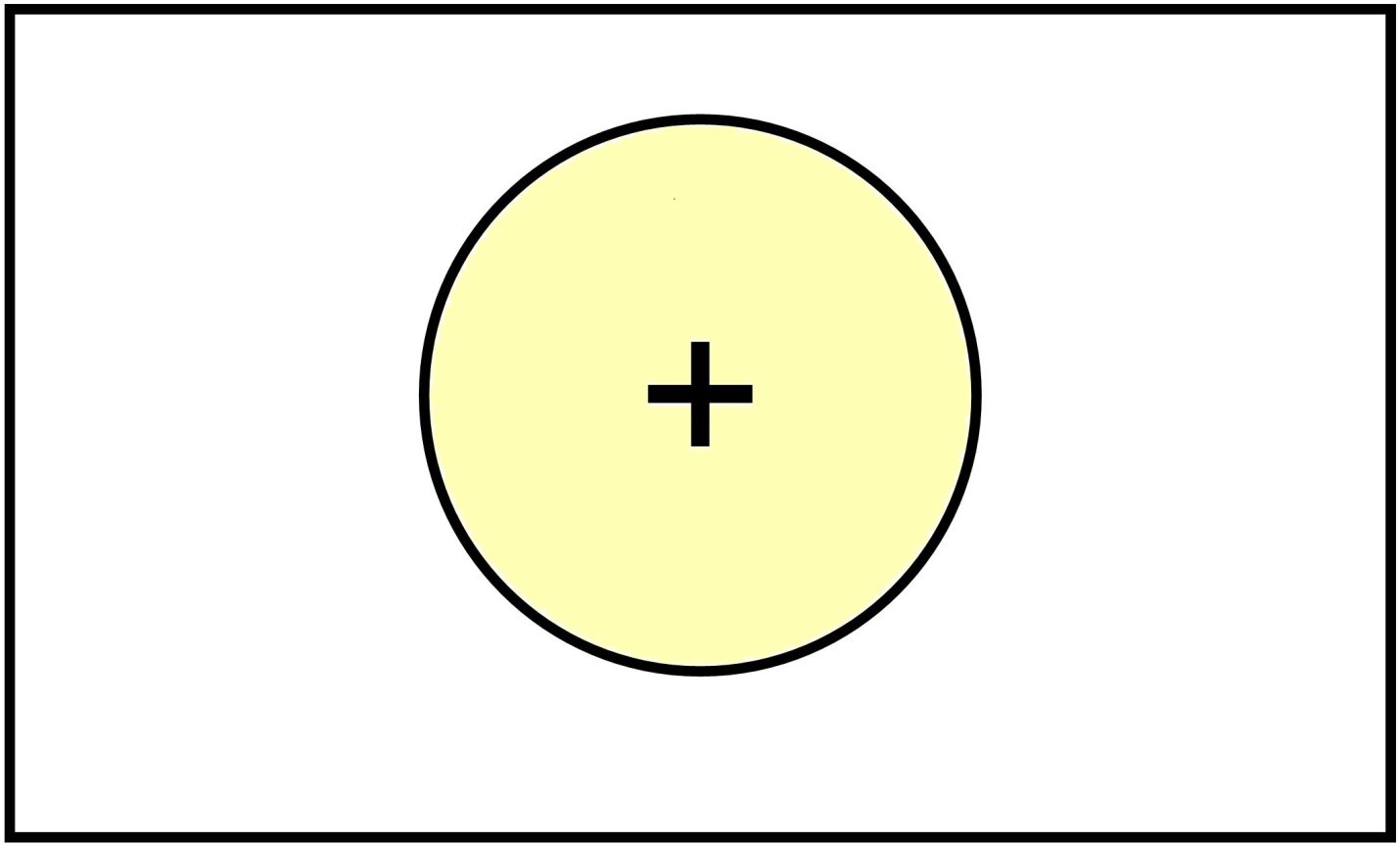
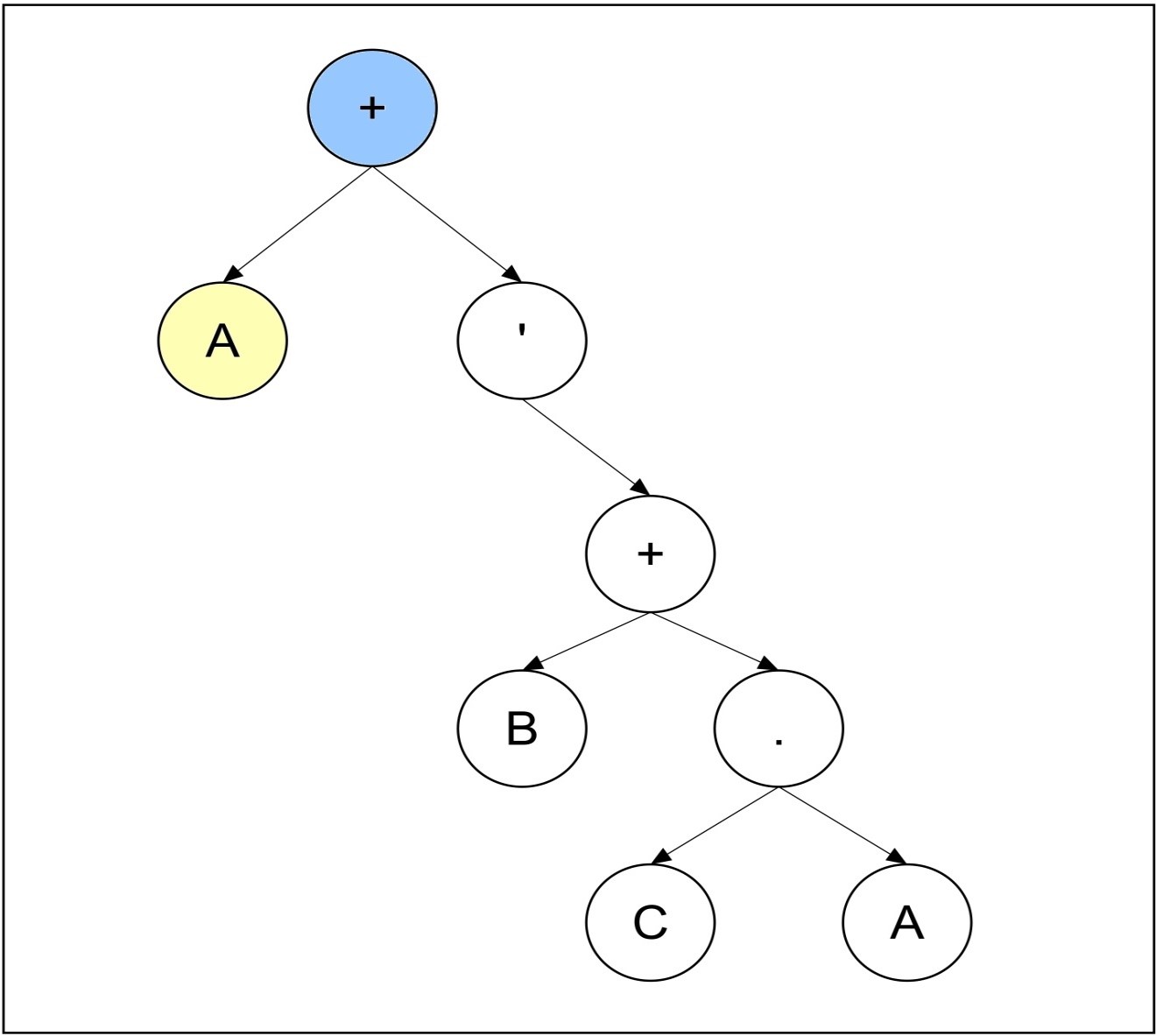
Step 1:
Expression: ABCA. + '+
As the Boolean expression is converted as the postfix expression, the expression will be read from right to left. The right most element of postfix expression is OR (+) operator. It is added as the root of the Boolean expression tree. The new added node is shown as faded yellow. The new added node is an operator, so the new added node will be current node after completion of 1st iteration.
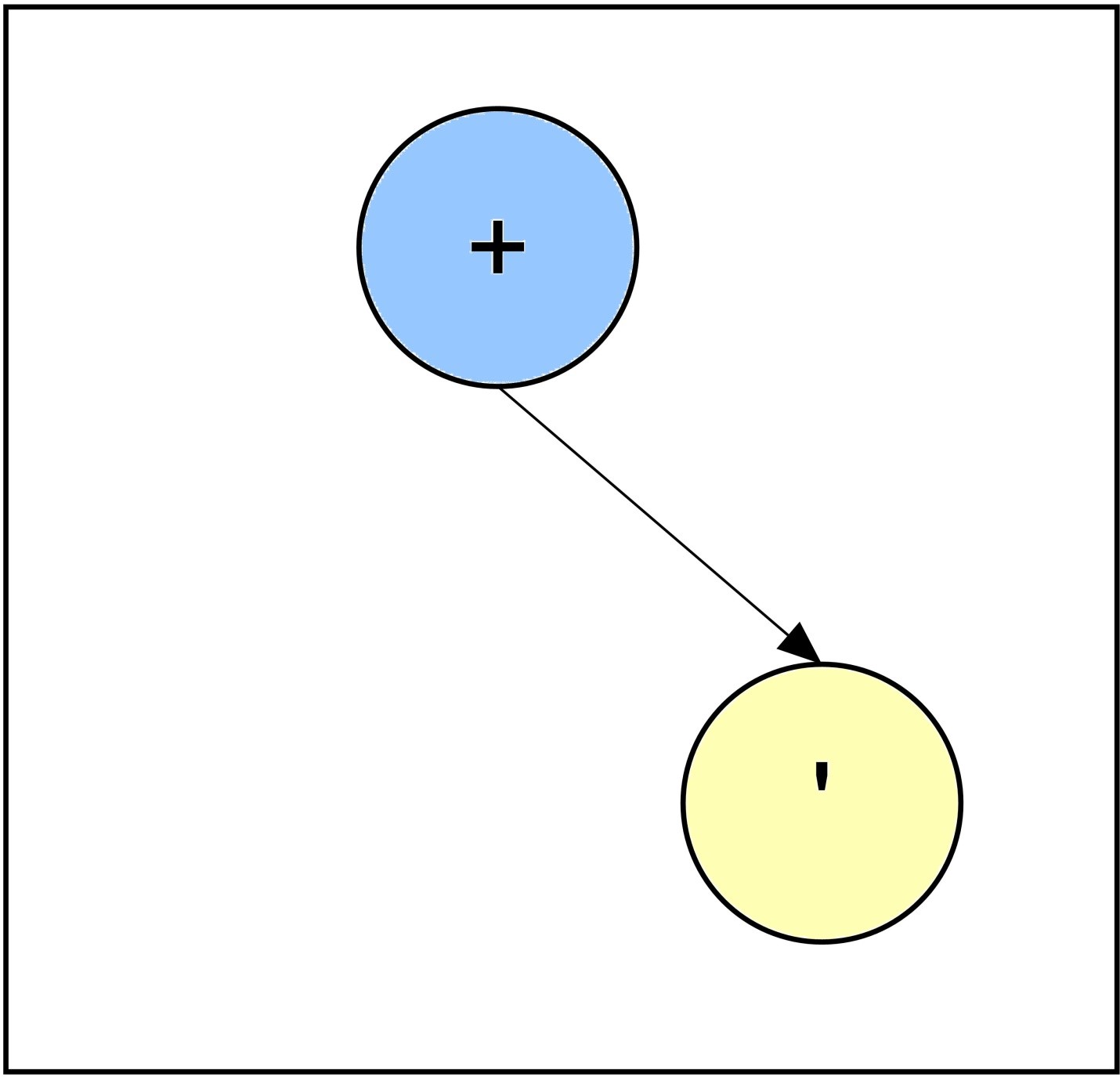
Step 2:
Expression: ABCA. + '+
As the right child of the current node is NULL, the NOT (' ) operator is added as the right sub child of the current node. The current node is shown as faded blue. The new added node is an operator, so the new added node will be current node after completion of 2nd iteration.
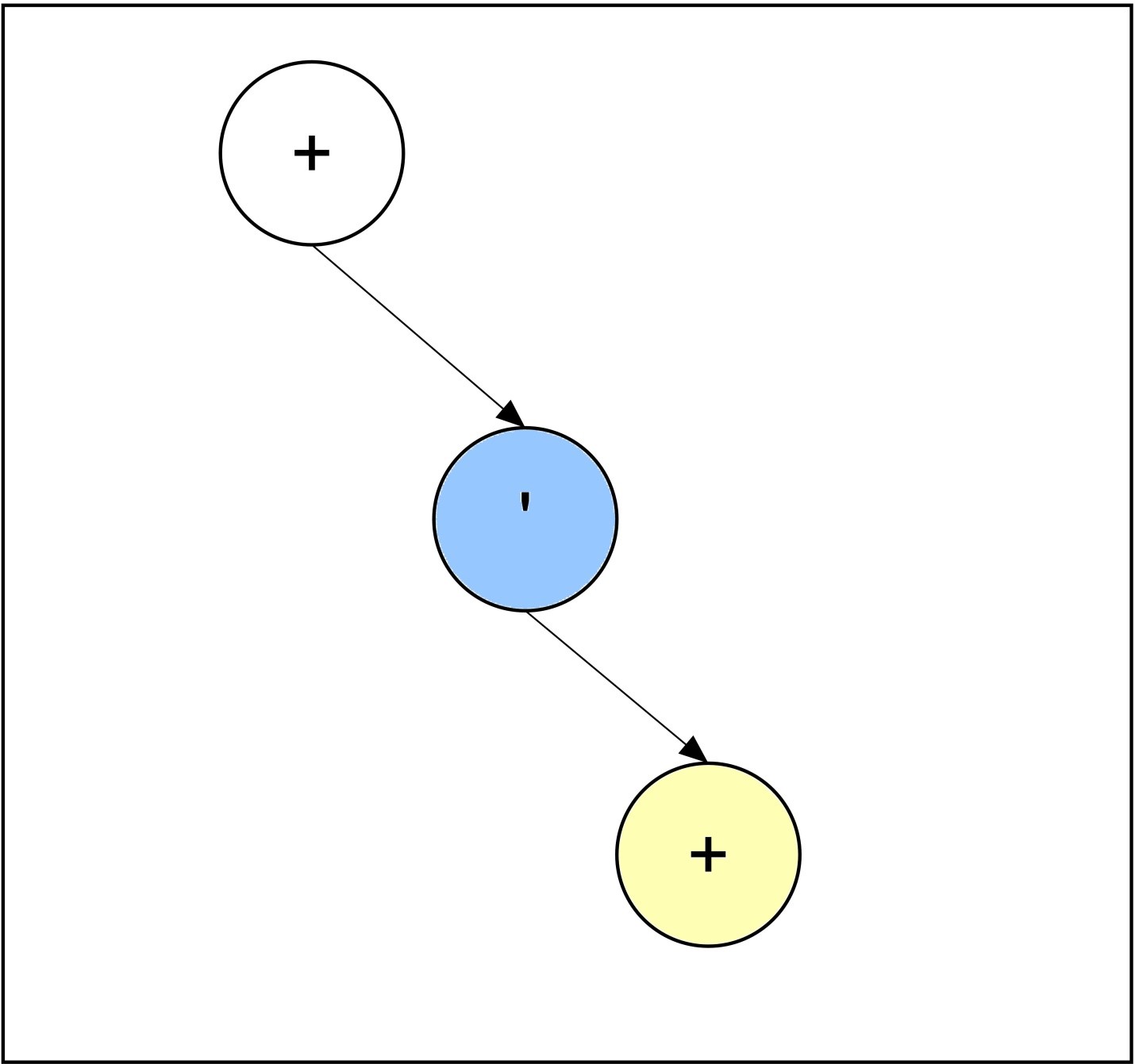
Step 3:
Expression: ABCA. + '+
As the right child of the current node is NULL, the OR (+) operator is added as the right sub child of the current node. The new added node is an operator, so the new added node will be current node after completion of 3rd iteration.
Step 4:
Expression: ABCA. + '+
As the right child of the current node is NULL, the AND (.) operator is added as the right sub child of the current node. The new added node is an operator, so the new added node will be current node after completion of 4th iteration.
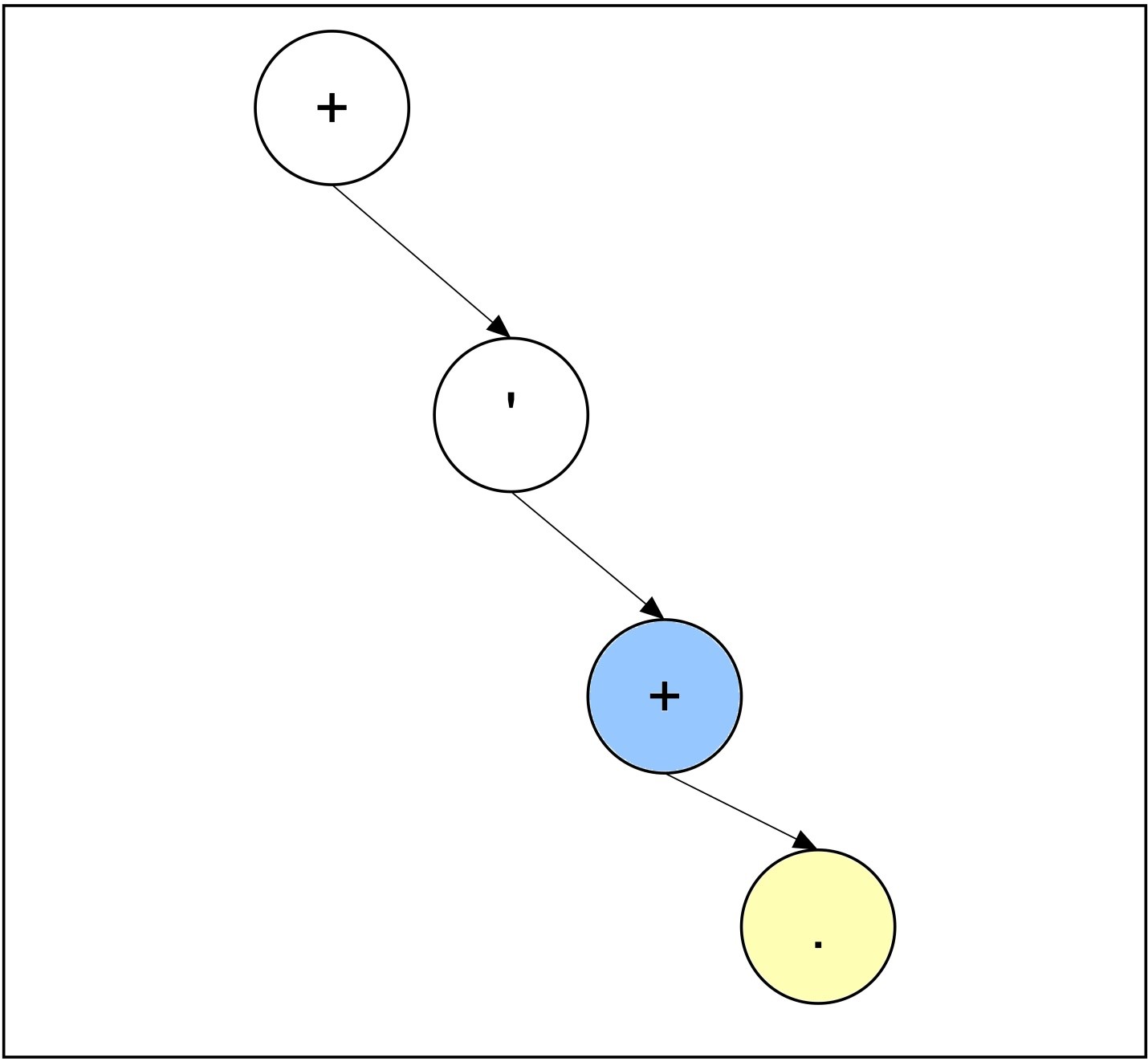
Step 5:
Expression: ABCA. + '+
As the right child of the current node is NULL, the operand A is added as the right sub child of the current node. The new added node is not an operator, so current node will not change, rather it will remain same after completion of 5th iteration.
Step 6:
Expression: ABCA. + '+
The right child of the current node is not NULL, but the left child of the current node is NULL. So, the operand C is added as the left sub child of the current node. The new added node is not an operator, so current node will not change, rather it will remain same after completion of 6th iteration.
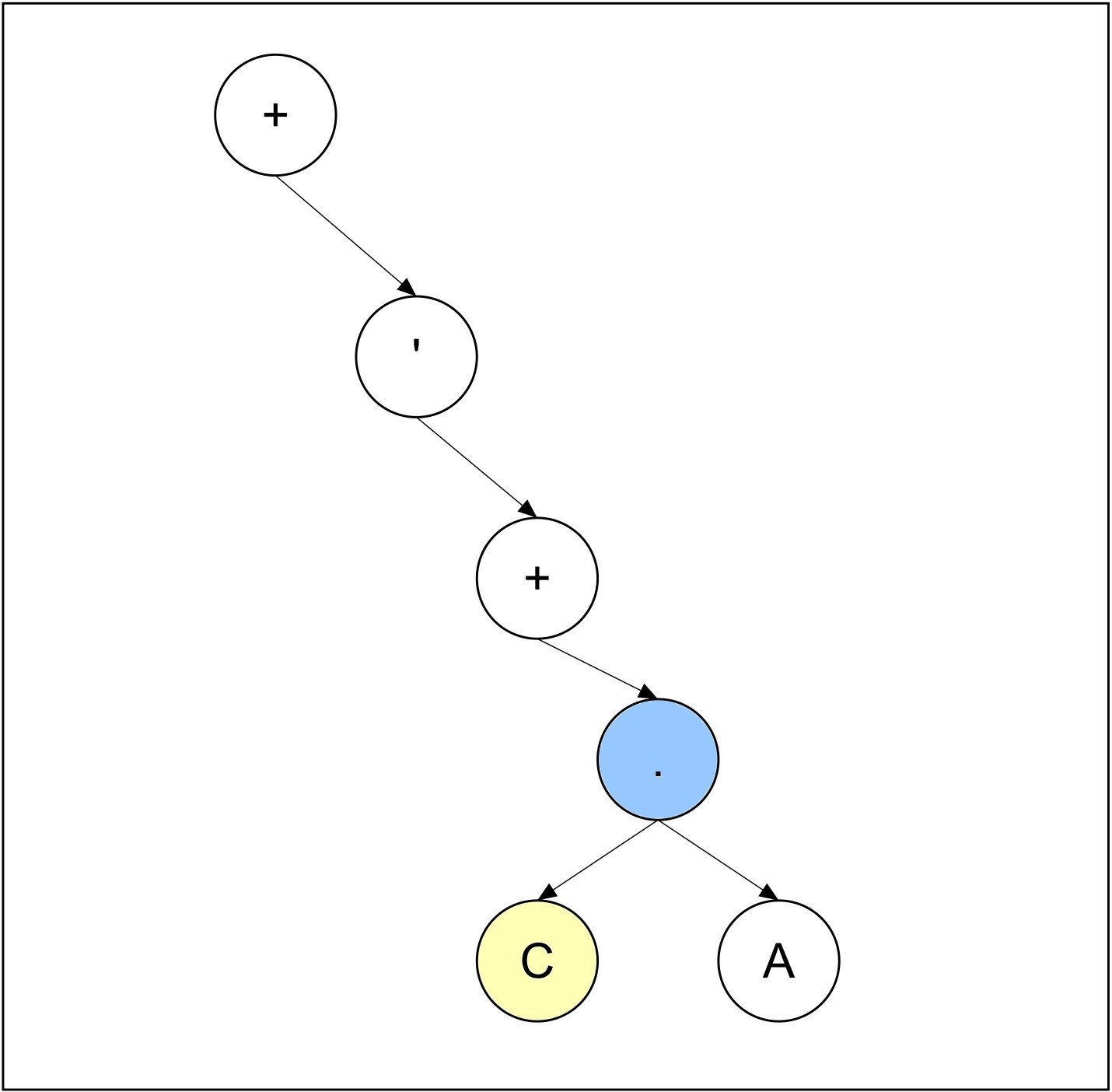
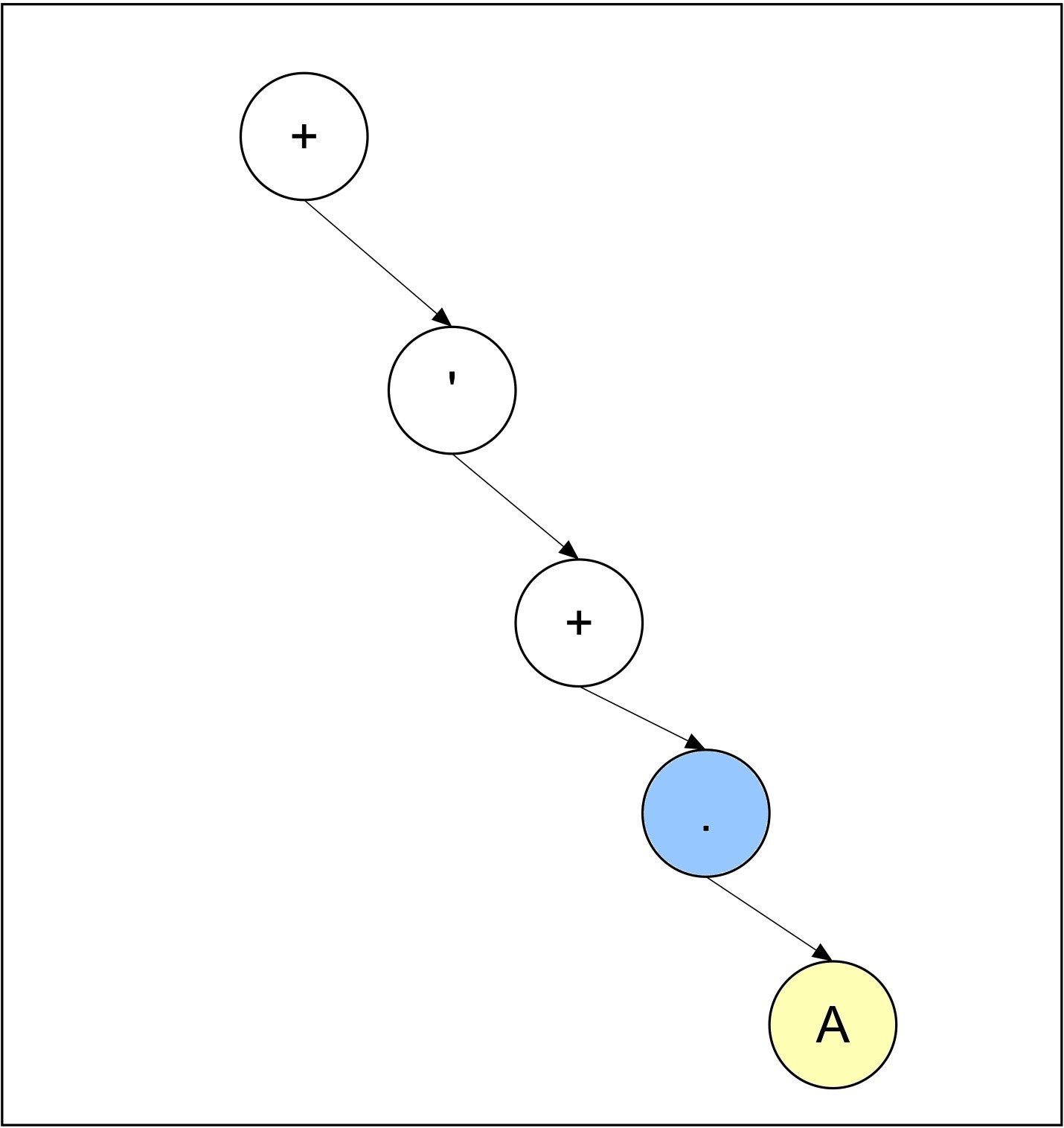
Step 7:
Expression: ABCA. + '+
Both right and left child of the current node are not NULL, So we will look for parent node which is containing less than or equal to two sub child and also containing a binary operator. The parent node of the current node is containing only one sub child, and the parent node is a binary operator, so the new current node will be the parent node of present current node. The operand B is added as the left sub child of the current node. The new added node is not an operator, so current node will not change, rather it will remain same after completion of 7th iteration.
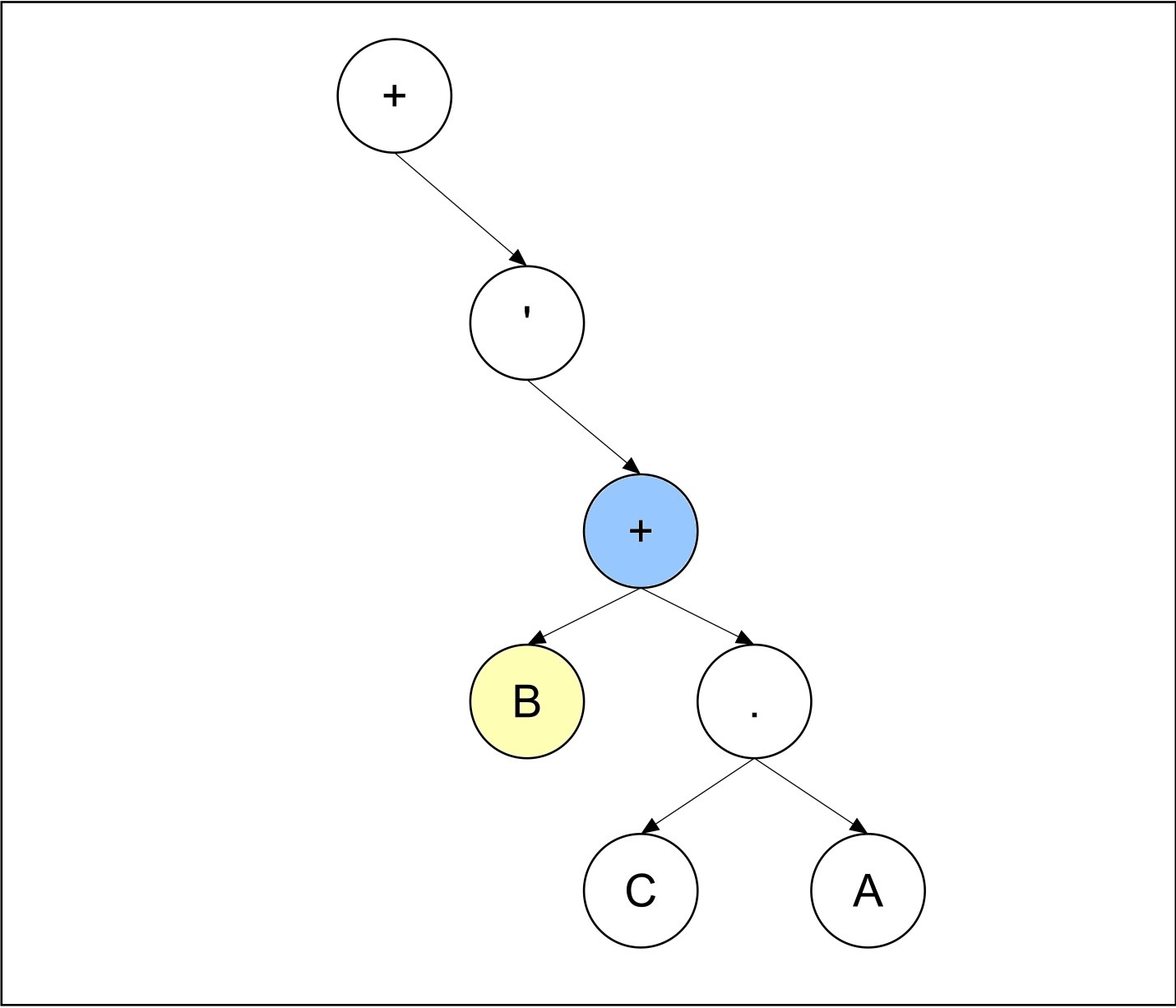
Step 8:
Expression: ABCA. + '+
Both right and left child of the current node is not NULL, So we will look for parent node which contains less than or equal to two sub child and also containing a binary operator. The parent node of current node is containing one sub child. But it is a unary operator and unary operators cannot have more than one operand so we will look for parent node again. The parent node of the parent node of the current node is containing only one sub child and, the node is containing a binary operator, so the new current node will be the parent node of parent node of present current node. The operand A is added as the left sub child of the current node. According to this example after completion of 8th iteration any operator and operand will not remain left, and the expression tree will be complete.
References
1. Bruno R. Preiss (1998). "Expression Trees". Retrieved December 20, 2010.
2. Marcus Fontoura Suhas Sadanandan Jayavel Shanmugasundaram Sergei Vassilvitski Erik Vee Srihari Venkatesan Jason Zien “Efficiently Evaluating Complex Boolean Expressions”
3. Wikipedia Expression tree.
